This paper was done by Matthew D. Zeiler while he was an intern at Google.

Introduction

The aim of many machine learning methods is to update a set of parameters $x$ in order to optimize an objective function $f(x)$. This often involves some iterative procedure which applies changes to the parameters, $\Delta{x}$ at each iteration of the algorithm. Denoting the parameters at the t-th iteration as $x_t$, this simple update rule becomes:

$$\Delta{x\_t} = - \eta{g\_t}$$

• $g_t$ is the gradient of the parameters at the t-th iteration
• $η$ is a learning rate which controls how large of a step to take in the direction of the negative gradient

Purpose

The idea presented in this paper was derived from ADAGRAD in order to improve upon the two main drawbacks of the method:

1. the continual decay of learning rates throughout training
2. the need for a manually selected global learning rate.

SGD vs ADAGRAD vs ADADELTA

• SGD: $\Delta{x\_t} = \rho{\Delta{x\_{t-1}}} - \eta{g\_t}$
  • where $\rho$ is a constant controlling the decay of the previous parameter updates
• ADAGRAD: $\Delta{x\_t} = -{ {\eta} \over \sqrt{\sum\_{T=1}^t g\_{T}^2} }$
• ADADELTA: $\Delta{x\_t} = -{ RMS\[\Delta{x}\]\_{t-1} \over RMS\[g\]\_t}g\_t$ $RMS[g]\_t = \sqrt{E[g^2]\_t + \epsilon}$ $E[g^2]\_t = \rho{E[g^2]\_{t-1} } + (1-\rho)g_{t}^2$
  • where a constant $\epsilon$ is added to better condition the denominator
  • where $E[g^2]_t$ is expected value of gradient with power 2 at time t

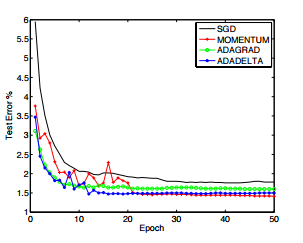
Result

Compared with SGD, ADAGRAD and MOMENTUM, normally ADADELTA has a convergence faster and has lower error rate.

Personal Thought

Have tried ADADELTA and SGD. Although for each epoch ADADELTA takes longer time to compute, we just have to input (default value) $\rho = 0.95$ and $\epsilon = 1e^{-6}$ then it will learn very well. If use SGD, we have to fine tune the learning rate and the error rate is often bigger than ADADELTA.